인공 신경망의 구조
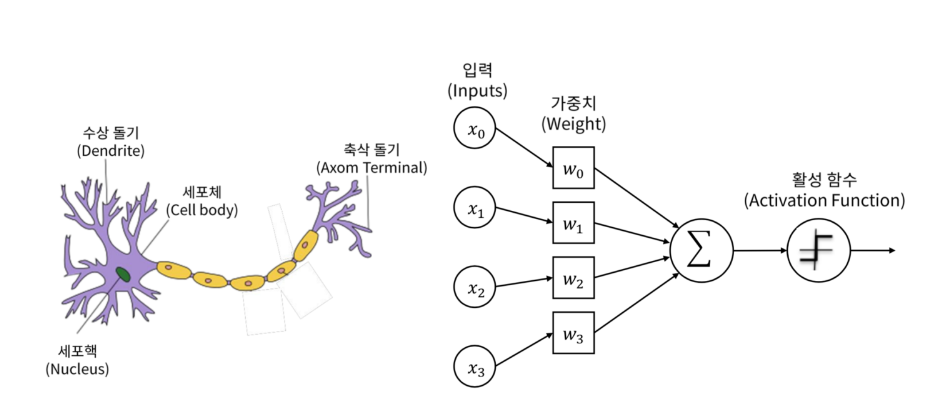
실제 뉴런의 원리를 응용하여 컴퓨터가 자동으로 학습을 할 수 있도록 한다.
- 수상 돌기 => 입력
- 시냅스의 연결 강도 => 가중치
- 입력 신호를 전부 합한다
- 세포의 역치 => 활성 함수
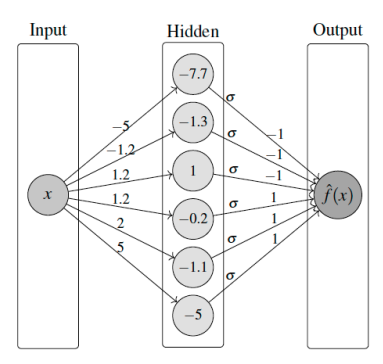
이런 형태로 뇌를 모방한다.
그런데 이때, 은닉층(Hidden Layer)가 2개 이상이면 일반적으로 딥러닝으로 부른다.
또한 뉴런들이 한줄로 쫙 한층만 있는것과 같은수여도 여러 층이 있는 경우의 차이는, 덜 민감해진다 할수있다.
지도 학습
지도 학습은 주어진 정답을 가장 잘 표현하는 함수를 찾는것으로, 이 학습은 주어진 정답과 예측한 정답의 차이를 줄이는, 다시 말해 손실 함수의 값을 0에 가깝게 만드는 과정이다. 손실 함수의 일종인 평균 제곱 오차(MSE)는 수식으로 이렇게 표현할수 있다.
$L=\frac{1}{3}((y_1-f(x_1))^2+(y_2-f(x_2))^2+(y_3-f(x_3))^2)$
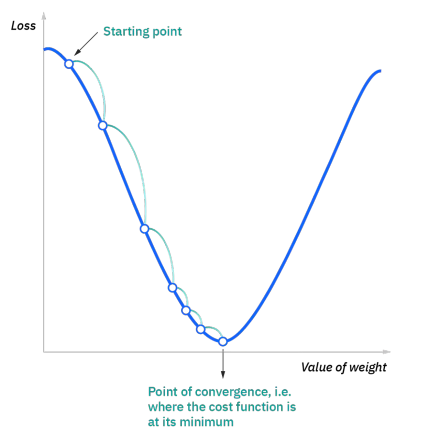
위 손실 함수는 2차 함수로 표현되며, 이를 미분하여 어느 방향으로 갈지 알아볼수 있으며, 이를 반복해 쭉 내려가 손실이 최소인 지점에 도달할 수 있다.
보편 근사 정리
하나의 은닉층을 갖는 인공 신경망은 임의의 연속인 함수를 원하는 정도의 정확도로 실행할 수 있다. 이 정리는 곧 인공신경망을 사용해서 모든 함수를 거의 정확하게 표현할수 있다는 것이며, 이는 인공신경망을 사용하는 이유가 될수있다.
인공 신경망을 통해 함수 예측하기
그렇다면, 인공 신경망을 $y=x^3+x^2-x-1$을 얼마나 정확하게 근사할 수 있을까?
import torch
import torch.nn as nn
import torch.nn.functional as F
import random
# Write neural network code
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.input_layer = nn.Linear(1, 6)
self.activation = nn.ReLU()
self.output_layer = nn.Linear(6, 1)
# 레이어 지정
def forward(self, x):
x = self.input_layer(x)
x = self.activation(x)
x = self.output_layer(x)
return x
# Define the network and the loss function.
network = NeuralNetwork()
loss_function = nn.MSELoss() # 손실함수를 MSE로 설정
# Steps for gradient descent.
# 'lr' stands for learning rate.
optimizer = torch.optim.Adam(network.parameters(), lr=0.001)
# Training one step with sample data
x = torch.Tensor([1]) # 1을 입력해서 테스트
y = x**3 + x**2 - x - 1 # 함수
optimizer.zero_grad()
output = network(x)
loss = loss_function(y, output)
loss.backward()
optimizer.step() # 학습시키기
# Check parameters
parameters = network.input_layer.state_dict()
w = parameters['weight'] # e.g. [-5, -1.2, 1.2, 1.2, 2, 5]
b = parameters['bias'] # e.g. [-7.7, -1.3, 1, -0.2, -1.1, -5]
print(w)
print(b)
위 코드는 딥러닝 환경을 구현하고 학습이 되는지 테스트를 해본다.
from tqdm import tqdm
import matplotlib.pyplot as plt
# Define the network and the loss function.
network = NeuralNetwork()
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(network.parameters(), lr=0.01)
pbar = tqdm(range(10000), desc="Loss: --")
for epoch in pbar:
x = (torch.rand(1)-0.5)*10
y = x**3 + x**2 - x - 1
# y = x**4-14*x**3-83*x**2+168*x+540
optimizer.zero_grad()
output = network(x)
loss = loss_function(y, output)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
pbar.set_description(f"Loss: {loss.item():.3f}")
이후 10000회 랜덤값을 넣어주는 학습을 시켜줬고, 그 결과다.
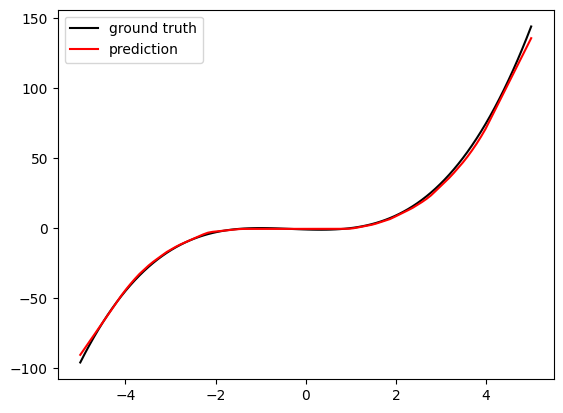
랜덤한 값이 입력되는 중간 부분은 학습이 제대로 진행되었지만, 양 끝부분은 그렇지 않다는 것을 볼수있다. 이는 학습이 진행되는 부분만 제대로 근사할수있다는것을 보여준다.
MNIST학습
그렇다면 조금 더 현실적인 학습을 시도해 본다. 손글씨 데이터셋을 통해 숫자를 구별하는 학습을 해볼것이다.
MNIST 데이터셋 받기
import torchvision
transform=torchvision.transforms.ToTensor()
train_data = torchvision.datasets.MNIST('./data', train=True, download=True, transform=transform)
test_data = torchvision.datasets.MNIST('./data', train=False, download=True, transform=transform)
학습
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.input_layer = nn.Linear(784, 1568)
self.activation = nn.ReLU()
self.hidden_layers = [nn.Linear(1568, 1568) for _ in range(1)]
self.output_layer = nn.Linear(1568, 10)
def forward(self, x):
x = self.input_layer(x)
x = self.activation(x)
for i in self.hidden_layers:
x=i(x)
self.activation(x)
x = self.output_layer(x)
return x
28*28의 그레이스케일 이미지를 784*1의 1차원 배열로 펼쳐서 학습한다. 1568개 뉴런을 가진 은닉층 1개와 10개의 출력이 있다.
from tqdm import tqdm
import matplotlib.pyplot as plt
import time
import random
import numpy
# Define the network and the loss function.
network = NeuralNetwork()
# loss_function = nn.MSELoss()
loss_function = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(network.parameters(), lr=0.01)
pbar = tqdm(range(50000), desc="Loss: --")
for epoch in pbar:
test_case=random.randint(0, 59999)
x = train_data[test_case][0].view(1, 784)
y = [0 for i in range(10)]
y[train_data[test_case][1]]=1
y = torch.Tensor(y)
y= y.view(1,10)
# time.sleep(1)
optimizer.zero_grad()
output = network(x)
loss = loss_function(output, y)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
pbar.set_description(f"Loss: {loss.item():.3f}")
이후 50000회 학습을 진행하였다.
성공률 확인
end=0
pbar = tqdm(range(5000), desc="Loss: --")
for epoch in pbar:
x = test_data[epoch][0].view(1, 784)
y = [0 for i in range(10)]
y[test_data[epoch][1]]=1
y = torch.Tensor(y)
y= y.view(1,10)
# time.sleep(1)
optimizer.zero_grad()
output = network(x)
loss = loss_function(output, y)
loss.backward()
optimizer.step()
output=output.tolist()[0]
if output.index(max(output))==test_data[epoch][1]:
end+=1
if epoch % 100 == 0:
pbar.set_description(f"Loss: {loss.item():.3f}")
print(end/epoch*100)
테스트 케이스를 진행하여 얻어낸 성공률은 70%이다.